Wave Secrets of
Our Health
The human body, has a coherent system that flexibly carries the flows of natural waves in our immediate environment. Everyday objects and apparels in our environment affect the wave coherence in our body’s biological system with metabolic and mutational consequences.
There are only two types of wave influences, either constructive or destructive.
The illustrations below show how this works in practice.
Constructive Wave Oscillation

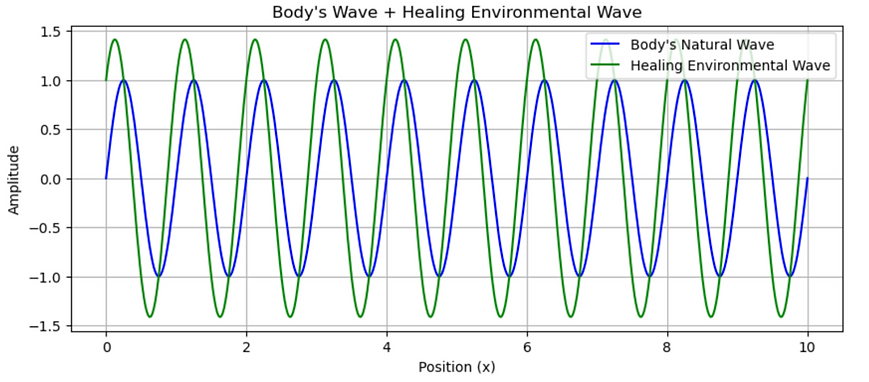
The illustration below shows the simple wave mechanisms of the first two constructive wave categories (Category 1 & 2) of everyday objects. They interact with each other favorably as constructive waves. This has a beneficial effect on our health and longevity and can help significantly in preventing chronic diseases.
The illustration below shows the simple wave mechanisms of the third and fourth destructive wave categories (Category 3 & 4) of everyday objects that interact as destructive counter waves which lower natural health waves. This weakens and destroys the immune system, accelerates the aging processes and imposes a variety of destructive vibrations on our cellular structures that can bring about the onset of certain chronic diseases.
Destructive Wave Interference

Constructive environment waves that are regenerative and rejuvenating. The diagram below shows how our body’s mechanisms interact with Healing Waves of environmental objects and trigger cellular resonance. The body waves have the potential to increase vibrations exponentially where the sum of the biofield waves and the constructive environmental waves is greater than 2 (1+1). When you have wave sum potentials of 4, 10, 50 or much higher counts (as shown in dashed lines below) greater than the regular body biofield, it will result in improved health and longevity.

Category 1: Healing QIW
Constructive Interference
Constructive waves that have a beneficial effect. Biocompatible waves of favorable items of clothing, furniture, bedding, jewelry, eyeglasses, dental materials etc constructively match the environmental standard of Health Frequency® and increase the balance of health and longevity. Favorable waves help create perceptible benefits to the natural features of genetic factors. Favorable or constructive QIW happen where waves of the body and the environment superimpose on each other to form a greater resultant amplitude. If the crest of one wave meets the trough of another wave, with the same magnitude of the same frequency at the same point, then the magnitude of the displacement is the sum of the individual magnitudes – this is constructive interference.
Category 2: Favorable QIW
Constructive Interference

Category 3: Average QIW
Destructive Interference

Destructive waves in our daily environment that lower the natural waves in our body The diagram below shows how our body’s mechanisms interact with Destructive QIW in the environment. The waves of the body and the waves in the environment superimpose on each other to form a lower resultant amplitude. When the natural body wave is 1.0 and the summand environmental waves is lower than 0, it lowers the body waves to below the natural condition of 1.0, where 0.x is the resultant interactions of a lowering environment. 1.0 + –0.x = 0.x always lowers the waves of the biofield and is therefore detrimental to health and longevity.
Category 4: Lethal QIW:
Destructive Interference

The diagram below shows how our body’s mechanisms interact with mortally destructive QIW in the environment. When the natural body wave is 1.0 and the counter environment’s waves is –1, the results of these wave interactions can, in a short time, lower the body waves to a dangerous condition, where 0 is the result of destructive environment wave interactions and lead to death. –1+ 1.0 = 0. Body waves that are aligned with Category 4 daily environmental waves are getting superimposed and form a near-zero resultant amplitude or negative resonance (as shown in dashed lines below). This can gradually or rapidly impair mitochondrial and cellular activity, disrupt the functionality and logistics of the signaling system, energy flow, and compromise the immune system’s defense mechanisms in the vitally important areas of our body. When the insulating properties of dental materials almost completely cut off the energy flow in active zones of the body, and the surrounding areas cannot compensate for these losses, exhaustion from hopeless trying to replenish the energy flow in the affected tissues can lead to seemingly inexplicable mortality.
Health Frequency (Ħ)
and Its Biological Interactions
Living organisms are complex systems that interact with their environment through various physical and chemical processes. Among these interactions, the role of waves—electromagnetic, acoustic, and quantum—has gained increasing attention. Health Frequency (Ħ) are mathematical models that describe how waves interact with biological systems, influencing cellular and systemic responses. These waves can be categorized based on their effects: healing (beneficial), favorable (neutral or mildly positive), destructive (harmful), and lethal (severely harmful).
Health Frequency (Ħ) represents a novel mathematical framework for understanding the mechanisms of interaction between environmental waves and biological systems with the logistic opportunity to take care of and control the behaviors of our health. This dissertation explores the theoretical foundations of wave interactions as a mathematical model for the experimental validation of Ħ. It categorizes them into healing, favorable, destructive, and lethal based on their wave effects on living organisms. By integrating quantum mechanics, electromagnetic theory, and cellular biology, this work provides a comprehensive model for how waves influence biological systems and proposes a robust experimental framework for validation. The findings have significant implications for medical science, material design, and environmental health.
First, we need to formally define in mathematical terms the essence of Health Frequency Waves:
Ħ(x,t) = A(x,t)·e^(iφ(x,t))
Or Ħ = A·e^(iφ)
The Equation of Biological Coherence
(Amplitude and phase of the body structures define the stability of life’s inner rhythm)
Where
-
A(x,t) is the amplitude function at position x and time t-tells us the strength of the wave
-
φ(x,t) is the phase function-tells us about its timing or alignment.
-
i is the unit
Category 1 (Healing wave):
Ħ₁(x,t) = B(x,t) + E(x,t) + k₁·B(x,t)·E(x,t) + R₁(x,t)·cos(θB - θE)
Or Ħ₁ = B+ E + k₁·B·E + R₁·cos(θB - θE)
Where:
B(x,t) is the body's natural wave function
E(x,t) is the environmental wave function
k₁ is the positive resonance coupling constant (>1) which amplifies the effect.
R₁ is the resonant amplification function
θB and θE are the phase angles of body and environmental waves
The cosine term creates maximum amplification when waves are in phase
Category 2 (Favorable wave):
Ħ₂(x,t) = B(x,t) + E(x,t) + k₂·min(B(x,t),E(x,t)) + R₂(x,t)·|cos(θB - θE)|
Or Ħ₂ = B + E + k₂·min(B,E) + R₂·|cos(θB - θE)|
Where:
-
k₂ is a moderate positive coupling constant (0<k₂<1)
-
R₂ is a smaller resonant function than R₁
|cos(θB - θE)|The absolute value ensures only constructive interference occurs

Category 3
(Destructive wave):
Ħ₃(x,t) = B(x,t) - |α·E(x,t)| + k₃·B(x,t)·E(x,t) + D₁(x,t)·cos(θB - θE + π)
Or Ħ₃ = B - |α·E| + k₃·B·E + D₁·cos(θB - θE + π)
Where:
-
α is an attenuation coefficient (0<α<1)k₃ is a negative coupling constant (-1<k₃<0)D₁ is a destructive interference function
-
The phase shift of π ensures waves are out of phase

Category 4
(Lethal wave):
Ħ₄(x,t) = B(x,t) - β·E(x,t) + k₄·B(x,t)·E(x,t) + D₂(x,t)·cos(θB - θE + π)·e^γt
Or Ħ₄ = B - β·E + k₄·B·E+ D₂·cos(θB - θE + π)·e^γt
Where
-
β is an amplification coefficient for destructive effects (β>1)k₄ is a strongly negative coupling constant (k₄<-1 )
-
D₂ is a stronger destructive function than D₁
-
γ is a time-dependent amplification constant
